안녕하세요. 라이징 크립토 고조입니다.
오늘은 다 공부하고 보면
참 사용하기 어려운 하모닉 패턴에
대해서 다뤄보도록 하겠습니다.
하모닉 패턴은 이론적인 진입가에서
진입하게 된다면 생각보다 아주 먼 손절가를 감당해야합니다.
패턴의 크기가 크면 클 수록 패턴 실패에 돌아오는
손실은 매우 클 수 밖에 없습니다.
또 이렇게 생각해봅시다.
지금까지 배웠던 패턴들의 반전 구간을 생각해보면서
공통적인 것을 생각해봅시다.
우리가 아는 패턴들의 진입가는 다음과 같습니다.
벳 패턴 0.886XA
알트 벳 패턴 1.13XA
샤크 패턴 0.886XA
가틀리 패턴 0.786XA
딥 가틀리 패턴 0.886XA
버터플라이 패턴 1.272XA
1.618 버터플라이 패턴 1.618XA
크랩 패턴 1.618XA
딥 크랩 패턴 1.618XA
B point와 진입가의 관계를 잘 생각해보면
0.382 -> 0.886XA(벳 패턴), 1.13XA(알트 벳 패턴), 1.618XA(크랩 패턴)

0.5 -> 0.886XA(벳 패턴),1.618XA(크랩 패턴)
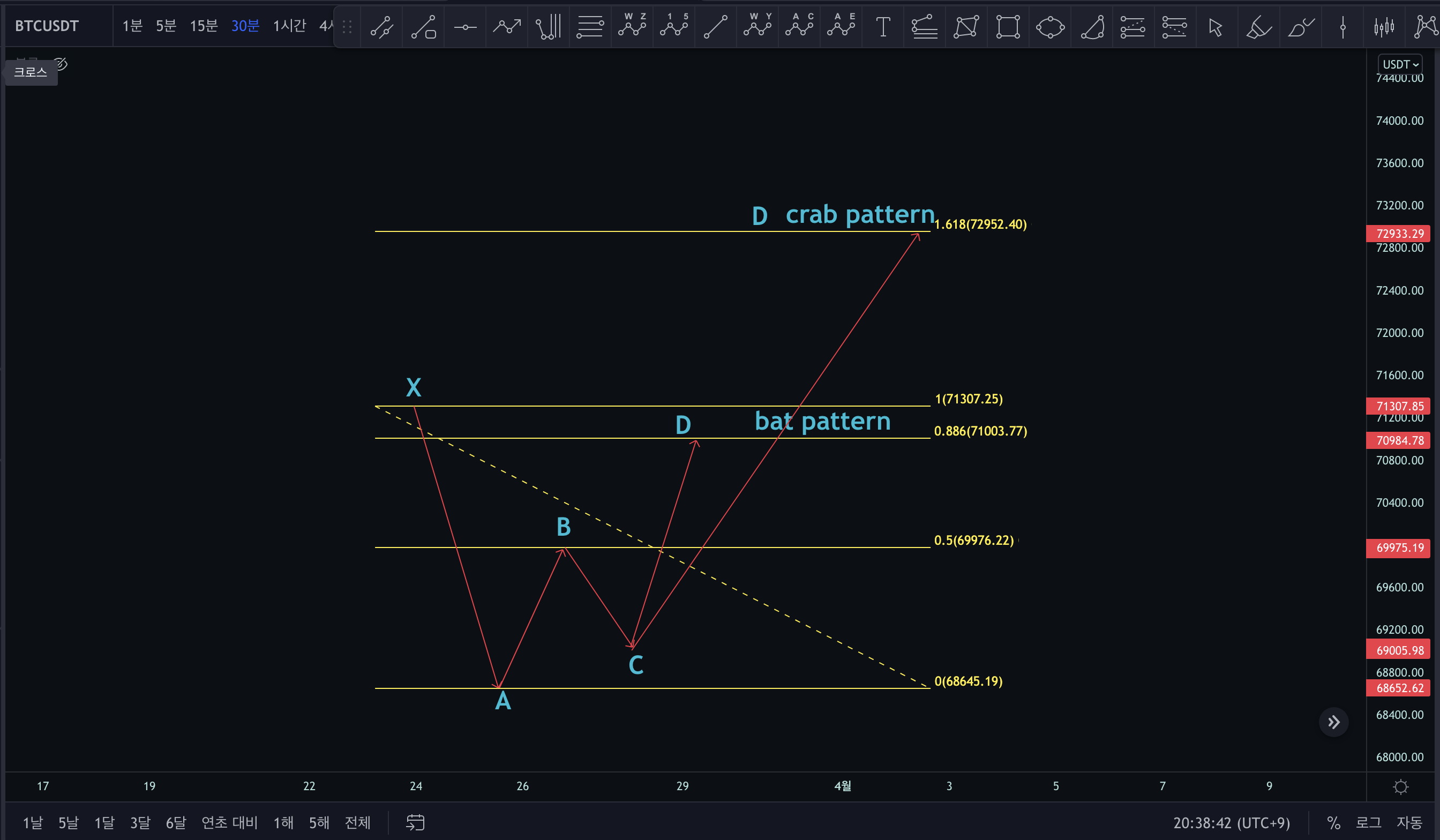
0.618 -> 0.786XA(가틀리 패턴), 0.886XA (딥 가틀리 패턴) , 1.618XA(크랩 패턴)

0.786 -> 1.272XA(버터플라이 패턴), 1.618XA(1.618 버터플라이 패턴)

0.886XA -> 1.618XA(딥 크랩 패턴)

교집합을 생각했을 때 모든 B POINT 구간에서 1.618XA는 고려가 되어야 합니다.
그러니까 B point의 범위 때문에 어느 정도 구별은 가능하지만
패턴을 다 공부해놓은 상태에서는
이젠 무슨 패턴을 어떻게 봐야할 지
정말 큰 고민이 듭니다.
그렇기에 우리는 이것을 해결하는 방법을 공부해야
하모닉으로 더 좋은 매매를 할 수 있게 될 것입니다.
제가 제시하는 방법은 네 가지 입니다.
첫째,
주요 피보나치 구간의 수렴
둘 째,
다른 근거들과 함께 패턴을 구분
셋 째,
경험을 많이하여 프렉탈 관점에서 패턴을 구분
넷 째,
여러가지 패턴이 완성되는 공통 구간 찾기
저는 절대 정답을 말 할 수 있는 사람이 아닙니다.
그리고 이 방법 말고도 더 좋은 방법이 있을 수 있습니다.
그래도 한 번은 들어봐 주시면 큰 도움이 될 거라고 생각합니다.
차근차근 다음 포스팅 부터 네 가지 이야기를 해볼까 합니다.
오늘도 긴 글 읽어주셔서 감사합니다.
'하모닉 패턴 > 하모닉 패턴 기본' 카테고리의 다른 글
| 하모닉 패턴의 활용) 추세선 (1) | 2022.02.09 |
|---|---|
| 하모닉 패턴의 활용) 여러 피보나치 구간의 수렴 (2) | 2022.02.09 |
| 하모닉 패턴) 5-point pattern과 BC PROJECTION (0) | 2022.02.09 |
| 하모닉 패턴) 5 POINT 패턴 - 파생 패턴 1.618 나비 패턴 (0) | 2022.02.09 |
| 하모닉 패턴) 5 POINT 패턴 - 파생 패턴 딥 크랩 패턴 (0) | 2022.02.09 |



