하모닉 패턴의 활용) 여러 피보나치 구간의 수렴
안녕하세요. 라이징 크립토 고조입니다.
오늘은 하모닉 패턴의 단점을 지우기 위한
피보나치 구간의 수렴에 대해서 알아보겠습니다.
지난 번 포스팅에서 말한
하모닉 패턴의 공통 진입가에 대한
고민 때문에 생기는 문제점을 해결하기 위한
첫 번째 방법은 피보나치 구간의 수렴입니다.
모든 패턴에서 B point는 매우 중요합니다만
패턴으로서 차트를 분석하려고만 하지 말고 모든 작도의 근본인
RETRACFEMENT와 PROJECTION 그리고
AB=CD 패턴의 수렴으로서만 차트를 분석해보는 것입니다.
이 때 우리가 중요하게 봐야할 피보나치 구간은
주요 피보나치 수와 주요 파생 피보나치 수인
0.618 0.786 0.886 1.13 1.272 1.618 이며
보조 파생 피보나치 수들인
0.382 0.5 0.707 1.414 2.0 2.24 등등은
중요도를 낮춰 보는 것입니다.
그럼 예시와 함께 설명 해보도록 하겠습니다.
총 예시는 4가지를 들어보겠습니다.
모든 시간은 한국 시간 기준입니다.
EXAMPLE 1) 2022년 2월 2일 1시
아래의 예시를 보시면
0.618AB=CD
1.618 projection
1.272 projection
1.13 projection
모두 겹치는 구간을 볼 수 있었고
굉장히 좋은 타점으로 볼 수 있었습니다.





EXAMPLE 2) 2021년 12월 28일 3시
아래의 예시를 보시면
1.13 projection
1.618 projection
1.272 projection들이
겹치는 구간으로 볼 수 있었고
좋은 타점으로 볼 수 있었습니다.




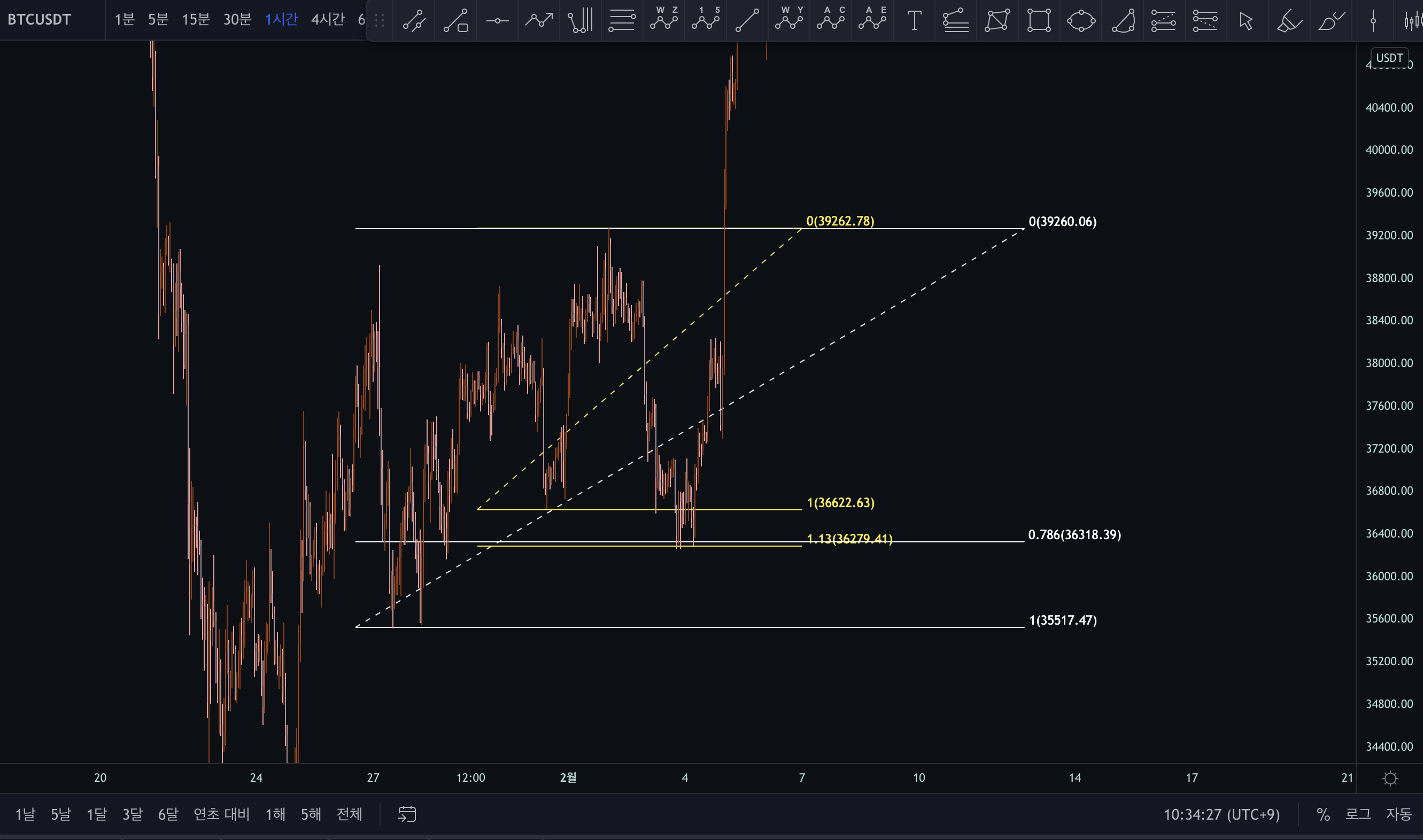
EXAMPLE 3) 2022년 2월 3일 21시
아래의 예시를 보시면
0.786 retracement와
1.13 projection가
겹치는 구간을 볼 수 있었고
좋은 타점으로 볼 수 있었습니다.


물론 구간의 패턴을 잘 들여다 보면 결국
크랩이나 대체 벳 패턴 등 하모닉 패턴을 찾을 수
있었겠지만
단순히 0.618 0.786 0.886 1.13 1.272 1.618 비율만으로도
하모닉의 근본인
AB=CD 패턴 ALTERNATE AB=CD 패턴
PROJECTION과 RETRACEMENT의 조합으로
재미를 볼 수 있다는 것이죠.
글을 마치며...
위의 6가지 비율은 정말
많이 나오는 비율입니다.
꼭 인지하시고 피보나치 구간의 수렴을
생각해보세요. 피보나치 만으로도
좋은 타점을 얻으실 수 있으실거에요.
이런 수렴의 예시들도 하나하나씩
더 업로드 하도록 하겠습니다.
오늘도 긴 글 읽어주셔서 감사하고
다음 포스팅에서는 두 번째 방법인
추세와 함께 하모닉을 사용하는 것에
대해 다뤄보겠습니다.
근데 제발 오해하지마요 ㅜㅜ
다른 보조 피보나치 비율들이 의미 없다는 소리는
절대로 절대로 아니니까요 ㅎㅎ 알았죠?
유튜브 영상 링크
위의 예시들을 영상으로 다시 정리 좀 했어요 ㅎㅎ
너무나도 중요한 이야기라서요 ㅎㅎ
다른건 안봐도 이영상은 진짜 꼭 봐줘요