안녕하세요. 라이징 크립토 도도입니다.
오늘은 AB=CD 패턴의 작도와 BC PROJECTION과 C RETRACEMENT에 대해서 다뤄보겠습니다.
AB=CD 작도와 BC PROJECTION, C RETRACEMENT
우선 AB=CD를 작도하기 전에 BC PROJECTION과 C RETRACEMENT를 이해하셔야합니다.
자 이미 PROJECTION과 RETRACEMENT를 다 이해하신 분들은 매우 쉬우실거에요.
우선 PROJECTION과 RETRACEMENT는 되돌림 피보나치 비율로 측정합니다.
그걸 인지하시고 다음 설명을 그림과 함께 이해해보셔요.
C RETRACMENT
이렇게 네 점이 있다고 생각합시다.
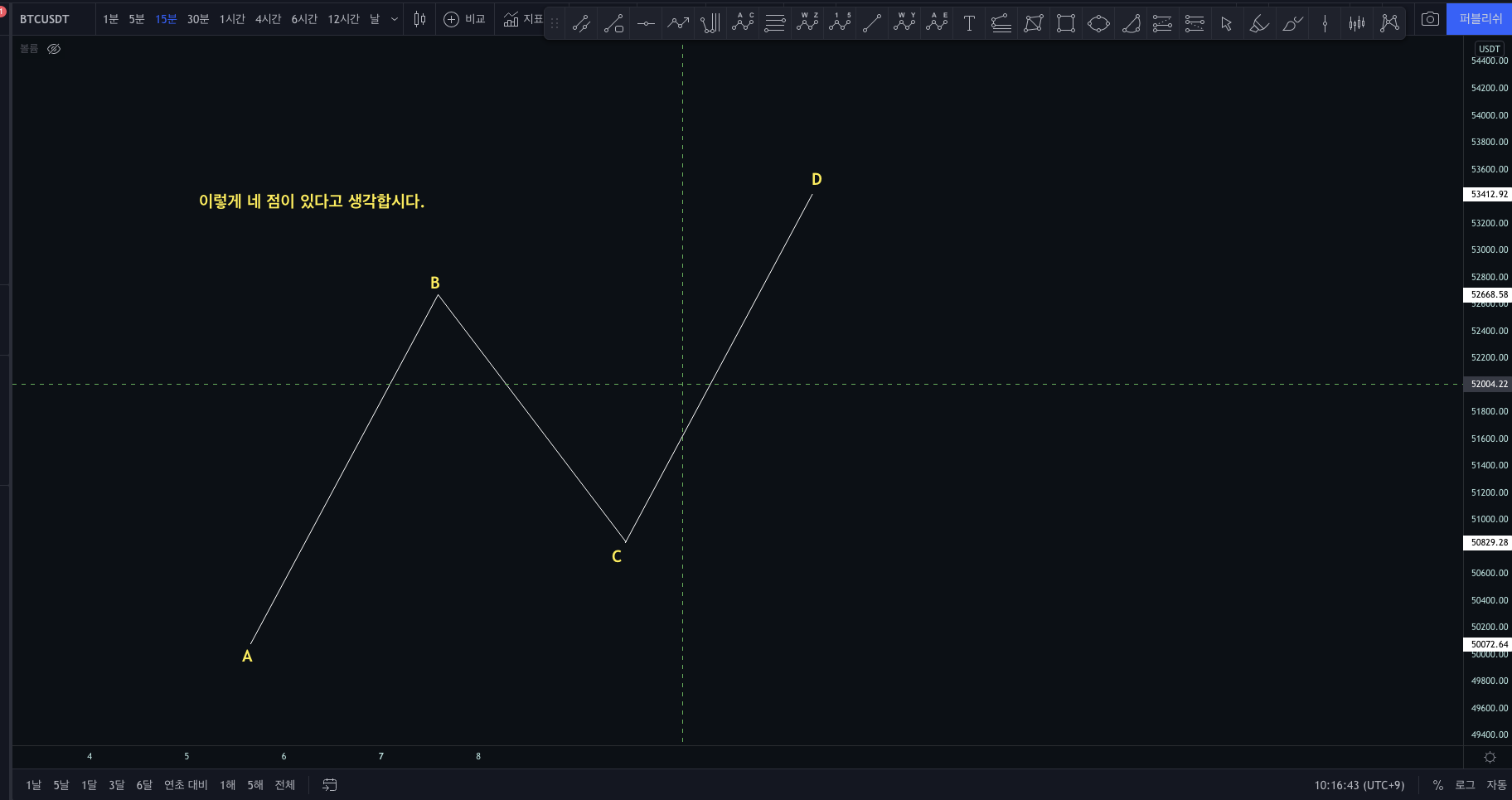
이때 C RETRACEMENT는 AB에 대한 C의 되돌림 비율 (C RETRACMENT RATIOS)을 의미합니다.
그렇다면 C RETRACEMENT는 AB에 대한 C POINT의 되돌림 비율이라고 생각하시면 되겠죠?
그리고 AB=CD패턴의 모양새를 보시면
C POINT는 1을 넘지 못한다는 것을 알 수 있습니다.
그래서 C RETRACEMENT라고 이해하시면 더 이해하기 쉬우실거에요.

그렇다면 이때 C RETRACEMENT는 0.707이 되겠죠?
어때요 참 쉽죠?

BC PROJECTION
이번엔 BC PROJECTION입니다. BC PROJECTION은 BC 선에 대한 D POINT의 되돌림 비율을 의미합니다.

즉 다음 그림에서 BC PROJECTION은 1.414이며 그 위치에 D POINT가 위치하는 것을 알 수 있습니다.

어떤가요? 자 이제 PROJECTION은 1을 넘는 비율들이니까
BC PROJECTION 값은 항상 B POINT를 넘어가서 존재하겠네요?
이런 생각도 해볼 수 있는 것이죠.
AB=CD 작도하기
자 이제 C RETRACEMENT와 BC PROJECTION을 이해하셨다면
AB=CD를 작도하기 위한 9부 능선은 넘어선 것 입니다.
이제 여기다가 하나의 과정만 더 추가를 한다면
우리는 AB=CD 패턴을 이용하여 차트를 분석할 수 있습니다.
그 작도 순서는 다음과 같습니다.
1.) A와 B를 설정합니다.
2.) 피보나치 되돌림 툴을 바탕으로 C를 설정합니다. (C RETRACEMENT를 찾는 것 입니다.)
3.) 피보나치 확장 툴을 바탕으로 1대1 즉 AB와 CD의 길이가 같은 구간을 측정하여 D구간을 특정합니다.
4.) BC PROJECTION을 측정하여 D 구간을 특정합니다.
5.) 확장 툴의 1대1 구간과 BC PROJECTION 값의 수렴 정도를 파악합니다.
그림과 함께 다시 한번 설명해보겠습니다.
아래를 보시죠.

C point를 C RETRACEMENT를 측정하여 정합니다.

그렇게 B와 C점이 정해지면 확장 툴을 이용하여 AB와 CD가
길이가 같은 점을 특정해봅니다.

BC PROJECTION을 측정해서 D POINT를 측정해봅니다.

자 이때 1.618 BC PROJECTION과 1대1 확장 비율이 수렴하는 것을 볼 수 있죠?

이렇게 수렴을 하게 되면 D POINT 예측의 신뢰도가 높아지며 반전이 일어날 가능성을 높게 볼 수 있습니다.
다시 한 번 정리하자면 C값이 나오면 BC PROJECTION과
1대1 확장 비율을 측정해서 D point를 예측해보는 것인거죠.
근데 여기서 궁금한 점이 생기실 수 있습니다.
그럼 어떤 비율을 봐야하는 건지에 대해서요.
여기서 우리가 생각을 해봐야하는 것이 1대1 확장 비율과
C RETRACEMENT 그리고 BC PROJECTION의 관계입니다.
1대1 확장 비율과 C RETRACEMENT 그리고 BC PROJECTION의 관계
결론부터 말씀드리자면
AB와 CD를 1대1로 만들어주는 C RETRACEMENT와 BC PROJECTION의 관계는 역수 관계입니다.
위의 작도 예시를 바탕으로 말씀드리자면
C RETRACEMENT RATIOS(C의 되돌림 비율)은 0.618 입니다.

AB=CD를 만족시켜주는 D점이 존재할 것 입니다.

그런데 여기서 CD선의 길이가 AB선의 길이를 같게 해주는 D point는 1/0.618BC PROJECTION입니다.
그리고 이 1/0.618을 계산해보면 1.618이나옵니다.
따라서 AB=CD를 만족하는 C RETRACEMENT와 BC PROJECTION의 관계 중 하나가
0.618과 1.618인 것이죠.

이렇게 확장과 C RETRACEMENT와 BC PROJECTION을 함께 적어보면 다음과 같습니다.
C RETRACEMENT가 0.618일 때 1대1을 만족시키는
BC PROJECTION은 그 역수인
(1/0.618=1.618)BC PROJECTION입니다.

다시 정리하자면 AB=CD 패턴에서 우리는 피보나치 확장툴과 피보나치 되돌림툴을 사용합니다.
그리고 AB=CD 패턴으로 우리가 매매를 하기 위해서는 D POINT (잠재적 반전 영역)을 예측하여 매매해야 합니다.
그럼 우리는 C POINT를 찾아서 되돌림 비율(RETRACEMENT RATIOS)를 측정한 후 그 역수 값의 BC PROJECTION을 찾은 후에
그 BC PROJECTION이 1대1 확장과 수렴을 하면 잠재적 반전 영역을 옳게 예측했다고 볼 수 있는 것이죠.
AB=CD 패턴을 만족하는 C RETRACEMENT와 BC PROJECTION 조합들
AB=CD 패턴을 만족하는 C RETRACEMENT와 BC PROEJCTION은
다음과 같이 정리 가능하며 서로 역수 관계입니다.
이렇게 상호적으로 AB=CD 패턴을 지켜주는 비율들을
AB=CD RECIPROCAL RATIOS라고 합니다.
|
AB에대한 C 되돌림 비율 (영어로 C RETRACEMENT)
|
BC PROJECTION
|
|
|
0.382
|
2.618
|
|
|
0.5
|
2.0
|
|
|
0.618
|
1.618
|
|
|
0.707
|
1.414
|
|
|
0.786
|
1.272
|
|
|
0.886
|
1.131
|
|
이 때 위의 빨간 색 표시가 되어있는 수들은 어떤 수들일까요?
주요 피보나치 수와 주요 파생 수인 0.618 0.786 1.272 1.618 이죠?
이 비율로 이루어진 AB=CD 패턴은 IDEAL AB=CD PATTERN이라고 하며
매우 높은 확률로 반전이 일어난다고 합니다.
글을 마치며...
오늘은 AB=CD 패턴의 핵심들을 알아보았습니다.
이 패턴 작도만 배워도 하모닉 90퍼세트 배운 겁니다.
지금 저 진지해요.
그러니 다음 포스팅까지 해서 마무리할 AB=CD 패턴은
필수적으로 숙지해주세요. 정말 도움이 많이 되실겁니다.
다음 포스팅에서는
ALTERNATE AB=CD PATTERN을 다뤄보도록 하겠습니다.
오늘도 긴 글 읽어주셔서 감사합니다.
'하모닉 패턴 > 하모닉 패턴 기본' 카테고리의 다른 글
| 하모닉 패턴) 5-POINT PATTERN의 특징 (2) | 2022.02.09 |
|---|---|
| 하모닉 패턴) 무엇보다도 중요한 AB=CD 패턴 (3) (1) | 2022.02.09 |
| 하모닉 패턴) 무엇보다도 중요한 AB=CD 패턴 (4) | 2022.02.09 |
| 하모닉 패턴) 패턴의 종류 (0) | 2022.02.08 |
| 하모닉 패턴의 기초) BEARISH & BULLISH (0) | 2022.02.07 |



